Hvordan skal vi forholde os til statistisk usikkerhed i kvalitetsvægtede gennemsnit af meningsmålinger? Jeg vil i dette indlæg forsøge at beskrive tre forskellige tilgange. Der vil være overlap med pointer bragt i tidligere indlæg, men mit sigte er primært at formulere, hvordan jeg over årene har rykket mig mere i retning af, at kvalitetsvægtede gennemsnit ikke kan bruges til at reducere den statistiske usikkerhed, vi ser i meningsmålingerne.
Et vigtigt aspekt af kvalitetsvægtede gennemsnit er at kvantificere usikkerhed – og i hvor høj grad vi tager tilfældige målefejl i betragtning (eller rettere sagt antager, at forskelle mellem meningsmålinger kan tilskrives tilfældige målefejl). Jeg vil i den forbindelse se bort fra, at nogle kvalitetsvægtede gennemsnit slet ikke kvantificerer denne usikkerhed (se evt. dette indlæg fra 2021, hvor jeg skriver mere herom), men blot nævne, at kvalitetsvægtede gennemsnit som hovedregel bør formidles med statistisk usikkerhed.
Når vi forholder os til kvalitetsvægtede gennemsnit er vi primært interesseret i selve gennemsnittet, og kun i mindre grad usikkerheden omkring gennemsnittet. Hele idéen med et kvalitetsvægtet gennemsnit er dog ikke blot at reducere støj (ved at estimere et gennemsnit), men også at reducere usikkerheden. Når vi eksempelvis har to meningsmålinger i stedet for én, har vi som regel også at gøre med dobbelt så mange respondenter, hvorfor det giver god mening at kunne udtale sig med større præcision.
Det er dog ikke skrevet i granit, hvordan vi skal forholde os til denne usikkerhed. Jeg vil derfor her fokusere på hvad jeg betegner som henholdsvis den optimistiske, kritiske og pessimistiske tilgang til statistisk usikkerhed i kvalitetsvægtede gennemsnit. Rækkefølgen er ingenlunde tilfældig men afspejler i høj grad hvordan min egen tilgang til kvalitetsvægtede gennemsnit har rykket sig i løbet af det sidste dusin år.
Den optimistiske tilgang
Den optimistiske tilgang til et kvalitetsvægtet gennemsnit af meningsmålinger bygger på ideen om, at meningsmålingerne beror på svarene fra tilfældigt udvalgte vælgere, og den primære – hvis ikke eneste relevante forskel mellem målingerne er, hvilke tilfældigt udvalgte vælgere, der er inkluderet i målingerne. Derfor kan vi relativt let kvantificere, hvor stor usikkerhed, vi skal arbejde med (for en introduktion til statistisk usikkerhed i meningsmålingerne, se dette indlæg).
Hvordan kvantificerer vi den statistiske usikkerhed når vi udelukkende har at gøre med tilfældige målefejl på baggrund af simpel tilfældig udvælgelse? Det er simpelt. Vi smider tallene sammen fra de forskellige meningsmålinger og udregner den statistiske usikkerhed med de dertilhørende mindre konfidensintervaller. Hvis der er to meningsmålinger, der begge har spurgt 1.000 vælgere, og den ene meningsmåling giver et parti 24% af stemmerne og den anden måling giver et parti 26% af stemmerne, vil det vægtede snit give partiet 25% af stemmerne med en statistisk usikkerhed på 1,9 procentpoint (når vi arbejder med et 95% konfidensniveau).
Med andre ord tager vi med den optimistiske tilgang blot alle målingerne og smider dem sammen uden de store betænkeligheder. Jo flere meningsmålinger vi har, desto mindre vil den statistiske usikkerhed derfor også altid være i vores vægtede snit. Det betyder selvsagt ikke, at der ikke er flere aspekter, vi skal forholde os til, og vi kan hurtigt gøre det mere kompliceret, især når meningsmålingerne ikke er foretaget på samme tid og vi ønsker at vægte nye målinger højere. Dette har betydning for den reelle stikprøvestørrelse og dermed også den statistiske usikkerhed.
Det er absolut intet problematisk i og for sig selv i at bruge denne tilgang til at lave et kvalitetsvægtet gennemsnit. Tværtimod er der flere nævneværdige fordele. Det er en simpel og transparent procedure uden det store hokus pokus, der gør det relativt let at reproducere denne slags vægtede snit. Populære eksempler på denne slags vægtede snit i en dansk sammenhæng er mig bekendt Risbjerg-snittet og det nu hedengangne Berlingske Barometer.
Den kritiske tilgang
Den kritiske tilgang til statistisk usikkerhed i kvalitetsvægtede gennemsnit tager udgangspunkt i, at vi har at gøre med tilfældig støj og systematiske målefejl. Vi kan således ikke blot udregne et simpelt gennemsnit af, hvad meningsmålingerne viser. Vi skal tværtimod forsøge at tage højde for, at analyseinstitutterne potentielt systematisk over- eller underestimerer opbakningen til bestemte partier relativt til, hvad andre meningsmålinger viser.
Hvis vi eksempelvis har to nye meningsmålinger, der begge giver samme opbakning til et parti, men hvor et analyseinstitut har for vane at give partiet en større opbakningen, skal vi først korrigere for dette, før vi udregner gennemsnittet og den dertilhørende statistiske usikkerhed. Faste læsere vil såledels være bekendt med idéen om huseffekter i meningsmålingerne.
Her skal vi selvfølgelig huske på, at det faktum et analyseinstitut giver et parti en opbakning, der afviger fra hvad andre institutter viser, ikke er ensbetydende med, at det pågældende analyseinstitut tager fejl. Det er blandt andet derfor, at det giver mening at lave en distinktion mellem huseffekter og husfejl. Når vi laver et kvalitetsvægtet gennemsnit ønsker vi blot at korrigere for disse forskelle, så et snit ikke påvirkes af, hvilke analyseinstitutter, der har foretaget flest meningsmålinger.
Hvad betyder det i praksis? Hvis vi ikke korrigerer for huseffekter, vil et kvalitetsvægtet gennemsnit give større vægt til de institutter, der har foretaget de seneste meningsmålinger. Det vil i en dansk sammenhæng betyde at Voxmeters meningsmålinger får en større indflydelse på, hvad et kvalitetsvægtet gennemsnit viser (da de foretager ugentlige meningsmålinger for Ritzau). Når vi inkluderer huseffekter lader vi dermed ikke et gennemsnit ændre sig fra dag til dag alt efter, hvilke institutter, der har foretaget meningsmålinger i de dage.
Huseffekter kan være nyttige at tage i betragtning, især når 1) der er forskelle, der ikke kan forklares med tilfældig støj (i.e., forskelle, der ikke er normalfordelt omkring et gennemsnit) og 2) der er forskelle i frekvensen for, hvor ofte analyseinstitutterne gennemfører meningsmålinger. Begge disse forhold bliver mere aktuelle, desto flere analyseinstitutter, der gennemfører meningsmålinger. Med andre ord er huseffekter relativt ligegyldige, hvis der kun er få institutter, der ikke varierer i hvor ofte, de gennemfører meningsmålinger, og ikke afviger væsentligt fra hinanden i forhold til, hvor stor opbakningen er til de forskellige partier.
Der kan således være gode argumenter for ikke at anvende huseffekter i et kvalitetsvægtet gennemsnit. En af grundene er såkaldt herding, altså at institutterne forsøger at få deres meningsmålinger til at ligge så tæt som muligt på, hvad andre meningsmålinger viser. Eller som jeg beskrev det i et tidligere indlæg: “Kort fortalt skal vi med meningsmålingerne ikke kun være bekymret for outliers, altså ekstreme meningsmålinger, men også inliers, altså meningsmålinger, der alle ligger meget tæt på hinanden.”
Tag eksempelvis YouGovs meningsmålinger i forrige valgperiode for Nye Borgerlige. Her er min beskrivelse fra et tidligere indlæg omkring opbakningen til Nye Borgerlige i YouGovs målinger: “Hvad jeg finder interessant her er hvordan YouGov – nærmest fra dag til næste – viste et kæmpe fald til partiet, som ikke var at finde i andre meningsmålinger. Det kunne i min optik tyde på, at YouGov op til valget ændrede deres metode, så partiet lå tættere på Voxmeter og andre analyseinstitutter.” Hvis der generelt har været store forskelle mellem institutterne op til et valg, men disse forskelle reduceres drastisk på grund af herding i dagene op til et valg, kan det skabe skævheder i de estimater, der kommer fra et kvalitetsvægtet gennemsnit, når der korrigeres for disse systematiske forskelle, som ikke længere gør sig gældende.
Størrelsen på disse huseffekter vil have direkte indflydelse på, hvor stor usikkerhed, vi arbejder med i vores model. Det ændrer dog ikke på, at vi grundlæggende blot bygger på en model, hvor vi stadig antager, at når blot vi har korrigeret for de systematiske forskelle mellem analyseinstitutterne, får vi præcise estimater, der giver et godt bud på, hvor partierne står i meningsmålingerne. Vi tager derfor – som regel – stadig udgangspunkt i, at meningsmålinger med flere respondenter skal gives større vægt end meningsmålinger med færre respondenter.
Et eksempel på et kvalitetsvægtet gennemsnit, der estimerede opbakningen til partierne og den statistiske usikkerhed for partierne var mit eget snit for Jyllands-Posten og Politologi.dk (rest in peace). Der er mig bekendt ingen alternativer i skrivende stund, hvilket er ærgerligt. Og så længe vi har noget der hedder TV 2 og Megafon, der gør hvad de kan for at ødelægge denne slags initiativer (potentielt fordi det udstiller deres egen elendige journalistiske praksis), ser jeg kun ringe kår for denne slags snit.
Det er godt at være kritisk i forhold til, hvordan vi skal forholde os til den statistiske usikkerhed i et kvalitetsvægtet gennemsnit, herunder styrker og begrænsninger ved at inkludere huseffekter. I løbet af de seneste år er jeg dog blevet mere og mere skeptisk til et punkt, hvor jeg vil betegne mig selv som værende pessimistisk.
Den pessimistiske tilgang
Hvorfor forsøger vi at bruge enkeltmålinger til at sige noget om den statistiske usikkerhed i vægtede snit? Giver det mening at tolke på 95% konfidensintervaller, troværdighedsintervaller m.v.? Jeg er stor tilhænger af at kvantificere graden af usikkerhed, og alternativet er trods alt værre. Vi kan altid øge usikkerheden i vores vægtede gennemsnit til et punkt, hvor det ikke alene er utroværdigt, men også ubrugeligt.
Jeg kan sige at vi med 100% sikkerhed ved, at opbakningen til et parti i en meningsmåling ligger et sted mellem 0 og 100%, men så er vi tilbage til start. Jeg læste eksempelvis et arbejdspapir, der giver et bud på, hvordan vi kan tage systematiske fejl i form af non-response i betragtning i udregningen af den statistiske usikkerhed. Deres primære eksempel viser, at opbakningen til Trump i en meningsmåling er 50.1% ± 49.3%, når man tager non-response i betragtning. Det er heldigvis kun et udgangspunkt til at vise, hvordan man med mere information omkring non-response kan forbedre denne usikkerhed, men det viser ikke desto mindre, at det kan være utroligt svært at tage systematiske fejl i betragtning, når vi forsøger at sige noget fornuftigt om den statistiske usikkerhed.
Ligeledes kan man være af den overbevisning, at man slet ikke kan lave vægtede gennemsnit af meningsmålingerne, da deres metoder er vidt forskellige og det er derfor mere en statistisk øvelse uden direkte anvendelighed. Dette er eksempelvis et argument Megafon står på mål for (se mit seneste indlæg for en diskussion af dette). Dette er selvsagt ikke en overbevisning, jeg deler, men jeg er sympatisk i forhold til den pessimistiske tilgang i forhold til, hvor gode kvalitetsvægtede gennemsnit er, når vi tager metodiske forskelle og ligheder mellem analyseinstitutterne i betragtning.
Den primære grund til, at jeg er pessimistisk i forhold til usikkerheden i kvalitetsvægtede gennemsnit er den diametralt modsatte af, hvad Megafon synes. Problemet med kvalitetsvægtede gennemsnit er ikke, at analyseinstitutterne har forskellige metoder, men at der er for store ligheder i nogle af de begrænsninger, de har. Det har den direkte konsekvens, at den statistiske usikkerhed ofte er for optimistisk (i.e., alt for lille). Vi udtaler os med andre ord med for stor præcision. Konkret er min bekymring, at vi ikke nødvendigvis kan udtale os med større præcision, blot fordi vi har flere meningsmålinger i et snit. Som jeg eksempelvis skrev i et indlæg forud for folketingsvalget i 2022: “Jo flere meningsmålinger vi har, desto mere kan vi udtale os med sikkerhed. Har vi eksempelvis fem meningsmålinger, der alle giver Moderaterne 10%, kan vi være mere sikre på, at Moderaternes opbakning er 10%, end hvis der kun er én måling, der viser det. Det er dog her, at vi skal huske at være kritiske i forhold til vægtede snit af meningsmålingerne. Hvis meningsmålingerne tager systematisk fejl i den samme retning, vil et vægtet gennemsnit ikke korrigere dem, men blot give mere præcise fejl (hvorfor vi vil udtale os med større sikkerhed omkring noget, der er forkert). Jo mere omtale et vægtet snit får, desto mere skal du forholde sig kritisk til sådan et snit, og især de enkeltmålinger, der bliver brugt i snittet.”
Vi kan konkludere, at den statistiske usikkerhed er for optimistisk i enkeltmålinger. Vi antager at respondenterne er tilfældigt udvalgt, hvilket ingenlunde er tilfældet. Vi ved således – også fra folketingsvalg – at estimater fra meningsmålingerne i dagene op til valget ligger uden for den statistiske usikkerhed mere end 5% af gangene (se dette indlæg for mere information). Idéen om tilfældig udvælgelse er et ideal som analyseinstitutterne ikke kan leve op til i dag, selv hvis de forsøger.
Håbet med huseffekter er, at systematiske fejl vil udligne hinanden. Det vil sige at ét analyseinstituts udfordringer vil være anderledes end andre analyseinstutters udfordringer. Med andre ord vil systematiske fejl mellem analyseinstitutterne ikke korrelere. Derfor kan vi uden de store problemer arbejde med antagelsen om, at når gennemsnittet af huseffekterne er 0 for et parti i målingerne, vil vi have et fornuftigt bud på, hvor stor opbakning der er, til det pågældende parti. Problemet med usikkerheden i vægtede snit opstår derfor ikke af forskellige metoder, men ligheder i de udfordringer, institutterne alle står over for, når de skal gennemføre en repræsentativ meningsmåling. Meningsmålingerne på statsniveau under det amerikanske præsidentvalg i 2016 er et godt eksempel herpå.
Det handler dog om mere end blot en diskussion omkring i hvilket omfang og hvordan vi skal estimere og forholde os til huseffekter. Jeg er i overvejende grad ikke overbevist om, at vi kan gøre brug af gængse antagelser, når vi skal estimere den statistiske usikkerhed. Det handler især om stikprøvestørrelsens betydning og forskellen på små og store partier.
For det første står jeg gerne på mål for, at stikprøvestørrelsen er så godt som ubrugelig, når vi skal sammenligne forskellige meningsmålinger. En meningsmåling med 1.500 respondenter skal med andre ord ikke have en større vægt end en meningsmåling med 1.000 respondenter. Jeg vil langt hellere have en meningsmåling, der følger alle kunstens regler, men som “kun” har spurgt 1.000 vælgere, end jeg vil have en meningsmåling, der har formået at spørge 5.000 vælgere, men med mindre fokus på, hvilke vælgere, der er blevet spurgt.
For det andet er jeg skeptisk i forhold til, hvor meget større den statistiske usikkerhed skal være for store partier. Jo større opbakningen er til et parti i en meningsmåling, desto større vil den statistiske usikkerhed som bekendt være. Det kan dog også betyde, at hvis meningsmålingerne undervurderer opbakningen til et stort parti, vil vi have mindre usikkerhed, men tage mere fejl. Dette bliver kun forstærket, hvis der også er forskelle i, hvor mange respondenter, der er i de pågældende meningsmålinger.
Lad os eksempelvis kigge på opbakningen til Socialdemokratiet ved folketingsvalget i 2022. Her fik partiet som bekendt 27,5% af stemmerne, hvilket var mere end de fleste meningsmålinger viste. En meningsmåling fra Voxmeter med 4.577 respondenter fra 31. oktober gav Socialdemokratiet 24,2% af stemmerne (3,3% procentpoint fra valgresultatet). Den lavere opbakning kombineret med en stor stikprøve gav en statistisk usikkerhed på 1,2 procentpoint. En meningsmåling fra YouGov med 1.336 respondenter, ligeledes fra 31. oktober, gav Socialdemokratiet 27,6% af stemmerne (0,1 procentpoint fra valgresultatet). Den statistiske usikkerhed i denne meningsmåling for partiet var 2,4 procentpoint. Med andre ord havde meningsmålingen, der ramte opbakningen til Socialdemokratiet så godt som præcist, en statistisk usikkerhed, der var dobbelt så stor som den meningsmåling, der tog mest fejl.
Megafon offentliggjorde fire meningsmålinger i løbet af valgkampens sidste fem dage i 2022. Jo lavere opbakning de viste til Socialdemokratiet, desto mindre den statistiske usikkerhed. Men også en større meningsmålingsfejl. Dette blev kun forstærket af, at deres stikprøve var mere end dobbelt så stor i deres meningsmåling, hvor de gav Socialdemokratiet den laveste opbakning. Disse dynamikker taler for, at nogle af de parametre og antagelser vi anvender, når vi forsøger at kvantificere den statistiske usikkerhed, kan få os til at tro, at vi er tættere på sandheden, selvom det modsatte er tilfældet.
Den statistiske usikkerhed er større (i procentpoint) og mindre (i procent) for store partier, men virkeligheden bliver hurtigt mere kompliceret, når vi ikke har at gøre med meningsmålinger, der bygger på tilfældig udvælgelse af respondenterne (altså repræsentative meningsmålinger). Derfor er det også kun naturligt at overveje, hvordan vi kan forbedre den kvantitative grad af sikkerhed, vi ønsker at udtale os med.
Med den statistiske usikkerhed i et kvalitetsvægtet gennemsnit forsøger vi at give et bud på, hvor sikre vi er på, at usikkerhedsintervallet indeholder valgresultatet (eller i en frekventistisk model, hvilken andel af valgresultaterne – når vi gentager folketingsvalget igen og igen – der vil ligge i konfidensintervallet). Noget jeg har tænkt meget over på det seneste er, om vores tiltro kan og bør informeres af vores viden omkring tidligere valg. Det kunne eksempelvis være et sandsynlighedsinterval, hvor vi er 95% sikre på, hvis meningsmålingerne klarer sig på niveau med tidligere valg, at et sandsynlighedsinterval indeholder det endelige valgresultat.
Der er intet ekstremt i at overveje meningsmålingernes succes ved tidligere valg, når vi laver et kvalitetsvægtet gennemsnit Det er eksempelvis noget FiveThirtyEights vægtede snit også tager højde for i deres pollster rating, når de taler om empirisk præcision: “The first is empirical accuracy, as measured by the average error and average bias of a pollster’s polls. We quantify error by calculating how close a pollster’s surveys land to actual election results, adjusting for how difficult each contest is to poll. Bias is just error that accounts for whether a pollster systematically overestimates Republicans or Democrats.”
En sådan rating giver dog ikke den store mening i en dansk kontekst, da meningsmålingerne generelt er af en meget høj kvalitet uden nævneværdige (parti)politiske skævheder. Ikke desto mindre kan jeg godt lide idéen om at kigge på tidligere valg, når vi ønsker at udtale os omkring, hvor sikre vi er på, at et vægtet snit kommer tæt på sandheden. Hvis meningsmålingerne eksempelvis ramte de seneste mange valg helt forbi skiven, hvorfor så forvente at de – uden væsentlig grund – skulle klare sig fantastisk ved næste valg?
Her er et hypotetisk scenarie: Forestil at vi havde et folketingsvalg én gang om ugen, altså 52 gange om året. Hvorfor ville vi ikke bruge alle disse folketingsvalg til at udtale os om den statistiske sandsynlighed for, at en meningsmåling rammer valgresultatet inden for et bestemt interval? Min pointe er her, at vores begrænsninger primært er af empirisk karakter, men det er et problem der bliver mindre, desto mere data vi har. Vi har selvsagt ikke mange folketingsvalg, men vi kan stadigvæk bruge tidligere resultater til at sige noget fornuftigt om sandsynligheden for, at et interval indeholder valgresultatet.
I nedenstående figur har jeg estimeret et vægtet gennemsnit af opbakningen til Socialdemokratiet fra den første meningsmåling efter folketingsvalget 2022 til i dag. Jeg tager også højde for huseffekter. Det relativt lille 95% usikkerhedsinterval omkring estimatet over tid er hvad min model fortæller er den statistiske usikkerhed. Det relativt store usikkerhedsinterval er intervallet der vil indeholde 95% af Socialdemokratiets meningsmålinger i dagene op til tidligere folketingsvalg (hvor jeg tager alle folketingsvalg fra 2001 til 2022 i betragtning). Det vil sige, at “kun” fem procent af meningsmålingerne for Socialdemokratiet, vil ligge uden for dette interval, hvis estimatet er præcist.
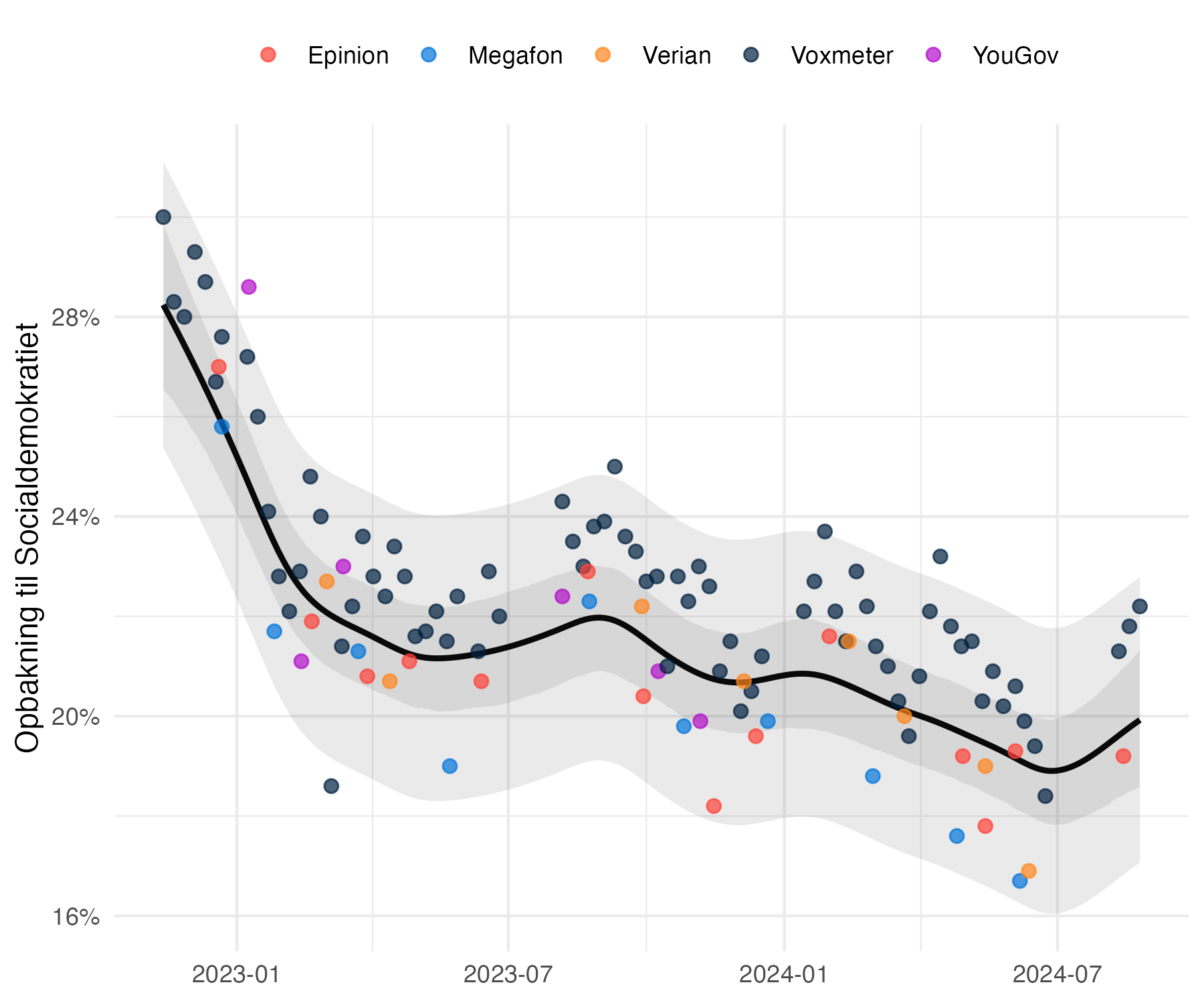
Min problem er, at modellen fortæller os at den statistiske usikkerhed er mindre end 2 procentpoint. Det var også et problem jeg havde med mit snit på Politologi.dk, altså at jeg ikke havde tiltro til, at vi kunne udtale os med så stor præcision. Med det “empiriske usikkerhedsinterval” opererer vi med en usikkerhed på ±2,9 procentpoint. Jeg har langt større tiltro til en usikkerhed på omkring 3 procentpoint end en usikkerhed, der er mindre end 2 procentpoint, med hvordan vi ved at meningsmålingerne klarer sig ved folketingsvalg.
Ovenstående er ikke udtryk for en færdig model, endsige proof of concept, men blot et forsøg på at illustrere nogle idéer, jeg har arbejdet med. Der er forskellige statistiske tilgange, der kan bruges til at kvantificere denne slags usikkerhed. Vi kan eksempelvis arbejde med conformal inferens, hvor tidligere forskelle mellem meningsmålinger og valgresultater bruges til at estimere 95% intervaller. En anden tilgang er at anvende empirical confidence interval calibration, hvor vi korrigerer vores konfidensinterval med udgangspunkt i den bias, vi estimerer vil være i meningsmålingerne.
Idéen er dog relativt simpel: Jo mere meningsmålingerne – samlet betragtet – har taget fejl i forhold til et parti ved tidligere valg, desto større usikkerhed. Jo mindre de har taget fejl, desto mindre usikkerhed. Der er dog begrænsninger, som er værd at forholde sig til, herunder nye partier, som vi ikke har nogen idé om, hvordan ville have klaret sig ved tidligere valg. Og så ved vi også, at de specifikke fejl vi er ved et valg, sjældent optræder ved næste valg (netop fordi analyseinstitutterne opdaterer deres metode på baggrund af tidligere udfordringer).
Det er dette jeg vil betegne som en pessimistisk tilgang, altså at vi i udgangspunktet antager, at meningsmålingerne ikke nødvendigvis er repræsentative, og primært forsøger at bruge viden fra tidligere valg til at udtale os om, hvor stor usikkerhed vi opererer med, når vi skal gøre os forhåbninger om, hvor sikre vi er på, at et gennemsnit vil ligge tæt på valgresultatet, hvis der var valg i dag.