Jeg faldt over dette fine indlæg af Morten Munster, hvori han beskriver 10 måder, medierne snyder med tal og statistikker. Det er som sagt et fint indlæg, men der var især én pointe, jeg er lodret uenig i.
Konkret beskrives det, hvordan y-aksen burde starte ved 0 i en figur, der viser antallet af danskere, der investerer i aktier over tid. Her er den figur, der bruges som eksempel i indlægget:
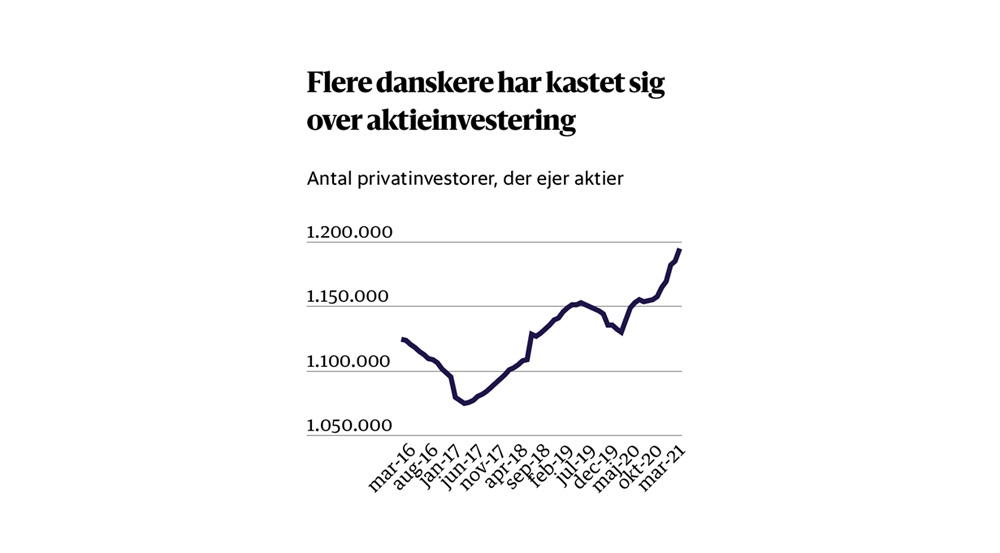
Argumentet er her, at det udelukkende er fordi der justeres på y-aksen, at man har en nyhed. Med andre ord ville der ikke være en nyhed, hvis y-aksen startede ved 0. Eller som det beskrives i forhold til, at y-aksen ikke starter ved 0: “Og hvorfor gør den så ikke det? Ja, det kan jeg godt fortælle dig. For så ville det jo grangiveligt ligne, at der faktisk ikke var nogen nyhed.”
Det er selvfølgelig muligt at manipulere med y-aksen for at få forskelle til at se større ud. Det er noget jeg blandt andet skrev et indlæg om for snart fem år siden. Det er dog oftest noget der primært sker, når man bruger søjlediagrammer, og det er ingen naturlov, at en linjegraf skal starte ved 0.
Faktisk vil jeg argumentere for, at det at starte y-aksen ved 0 i ovennævnte eksempel ville være en fejl, der ignorerer en aktuel nyhed. I indlægget skriver Morten Munster, at stigningen “går kun fra 1.050.000 til 1.200.000”. Der er trods alt tale om en stigning på omkring 14%! Det er ikke en lille stigning, og der er ingen grund til at vise 0 på en y-akse, i sådan en figur. Det er af samme grund, at du sjældent vil finde tidsseriegrafer over aktiekurser, der starter ved 0.
I indlægget gives der et eksempel på, hvorfor det er vigtigt, at y-aksen starter ved 0. Her kan man ganske rigtigt se, at linjegrafen ser fladere ud end i ovenstående figur:
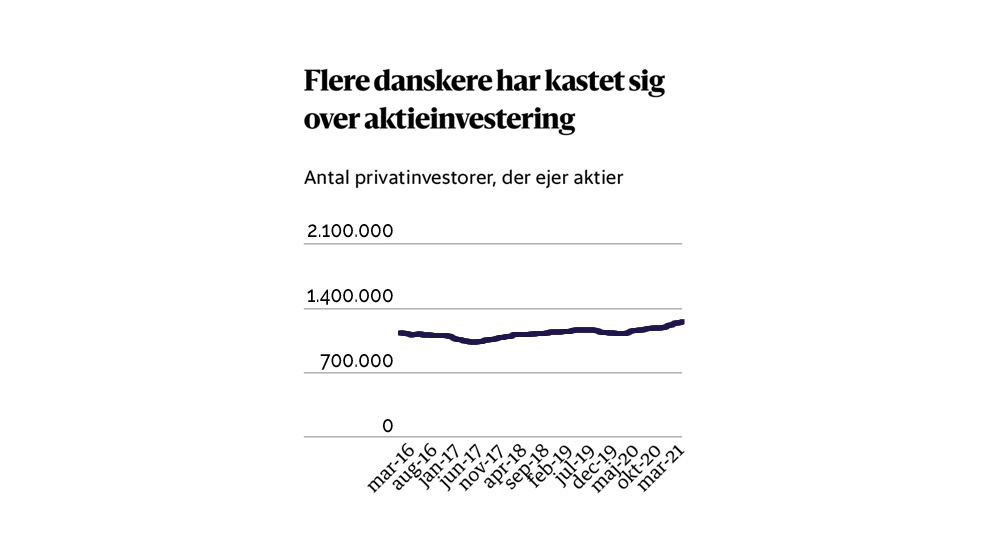
Jeg finder dette forslag til en forbedring værende alt andet end en forbedring. Mest problematisk er det, at ikke alene er 0 nu inkluderet, men y-aksen går hele vejen til +2 millioner danskere. En af grundene til at linjegrafen ser flad ud er dermed ikke alene, at y-aksen starter ved 0, men at der også er ændret på maksimumværdien.
Dette gør at selv en stigning på omkring 500.000 danskere ville se minimal ud med den “forbedrede” y-akse. Det fremhæver hvordan man kan ændre y-aksen til at få ændringer over tid til at se mindre ud, end de egentlig er.
Jeg brugte en del tid på dette spørgsmål for et par år siden, da jeg forsøgte at forbedre visualiseringen af partiernes opbakning i meningsmålingerne over tid (jeg skrev et indlæg om dette for her). Konkret endte jeg med at bruge et forslag af Francis Gagnon, der giver en god tommerfingeregel for, hvor ens y-akse kan begynde og ende, når man viser ændringer over tid i en figur.
Det korte af det lange er, at y-aksen ikke skal starte ved 0. Tværtimod kan der være meget gode grunde til ikke altid at starte en y-akse ved 0.