We cannot understand modern politics without studying social media. Politicians as well as ordinary citizens rely on social media to discuss and consume political content. One of the data sources researchers rely on to study behaviour on social media is survey data. However, there can be specific challenges with studying social media. Here, I will illustrate such a challenge when using survey data to study behaviour on social media. Specifically, even if you rely on a representative sample to study social media behaviour, there is no guarantee that you can use this sample to make meaningful inferences about social media users.
To understand this, we need to understand that there is a difference between the sample size you have and the sample size you end up using in your statistical models. If you have interviewed 1,000 citizens, but only 100 of these actually use social media, how much can we then actually say based on this data?
Research from the UK shows that users of Twitter and Facebook are not representative of the general population (see also this paper). However, there are even more potential problems with using survey data to study behaviour on social media. Specifically, we know that the “effective sample” is not necessarily similar to the real sample. That is, just because you have a specific sample, you cannot expect that estimates obtained from a regression will apply to the population that the actual sample is represenative for (see this great paper for more information).
I was thinking about this issue when I read a paper titled “Ties, Likes, and Tweets: Using Strong and Weak Ties to Explain Differences in Protest Participation Across Facebook and Twitter Use”. You can find the paper here. There are so different issues with the paper but I will focus on one particular issue here, namely the small sample we end up looking at in the manuscript and the implications hereof.
The paper examines whether people have strong and weak ties on Facebook and Twitter and how that matters for their participation in protest activities. Specifically, the paper argues that different types of social ties matter on Facebook and Twitter. The paper expects, in two hypotheses, that strong ties matter more for Facebook use in relation to protest behaviour whereas weak ties matter more for Twitter use in relation to protest behaviour. This is also what the paper (supposedly) finds empirical support for. Here is the main result presented in Table 1 in the paper:
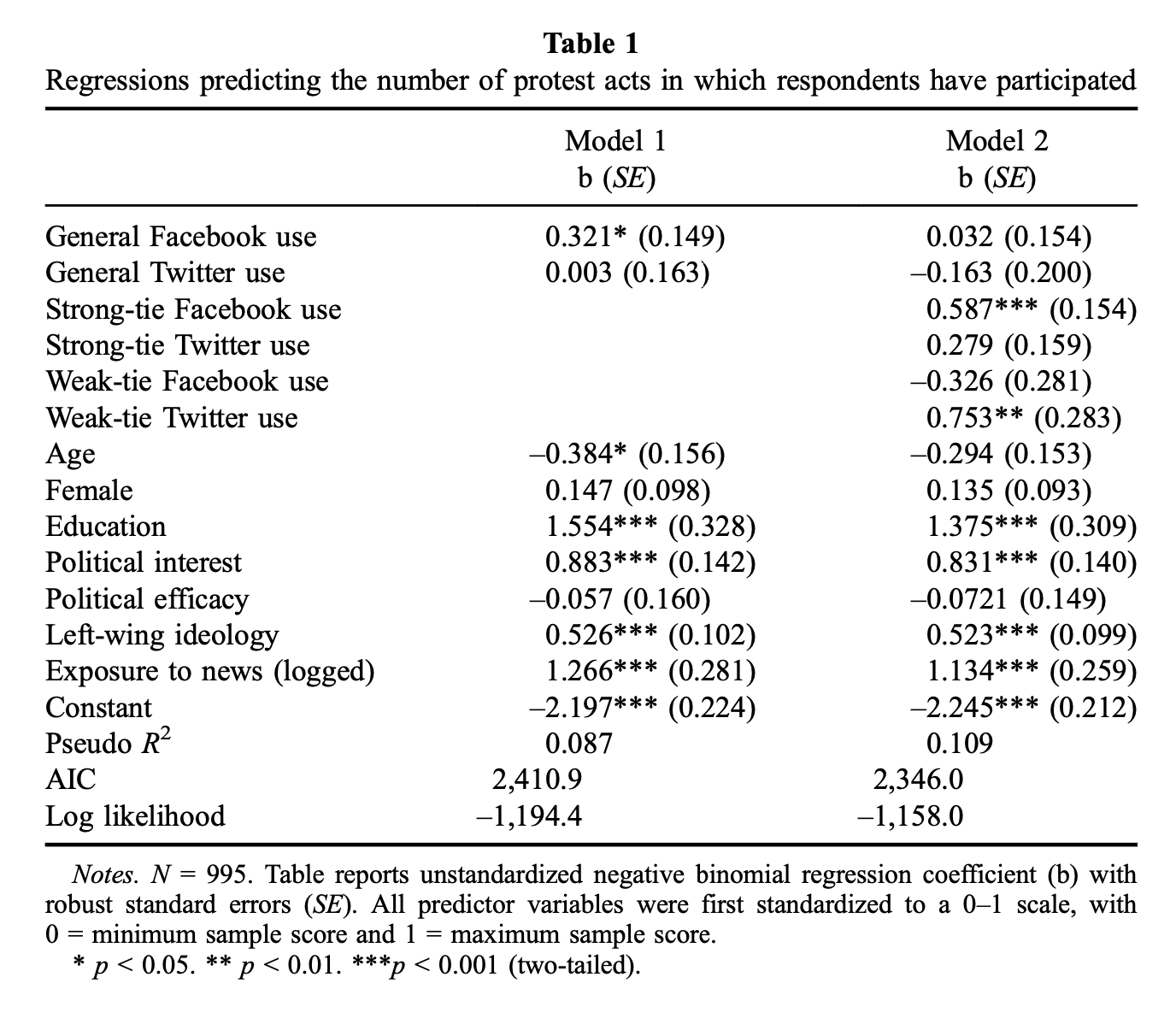
That’s a lot of numbers. Very impressive. And look at that sample size… 995! But here is the problem: While the paper relies on a representative survey with 1,000 respondents, only 164 of these respondents use Facebook and Twitter. You could have had a sample size of 100,000, but if only 164 of those used Facebook and Twitter, how much should be believe that the findings generalise to the full sample?
Out of the 164 respondents using Facebook and Twitter, only 125 have weak or strong ties. And only 66 of the respondents have variation in the ties within the respective social media platform (i.e. not the same weak or strong ties on Facebook or Twitter). Only 18 respondents in the sample have different ties across the respective social media platforms (i.e. not the same weak or strong ties on Facebook and Twitter). Here is a figure showing how we end up with only having variation on the relevant variables for 2% of the sample:
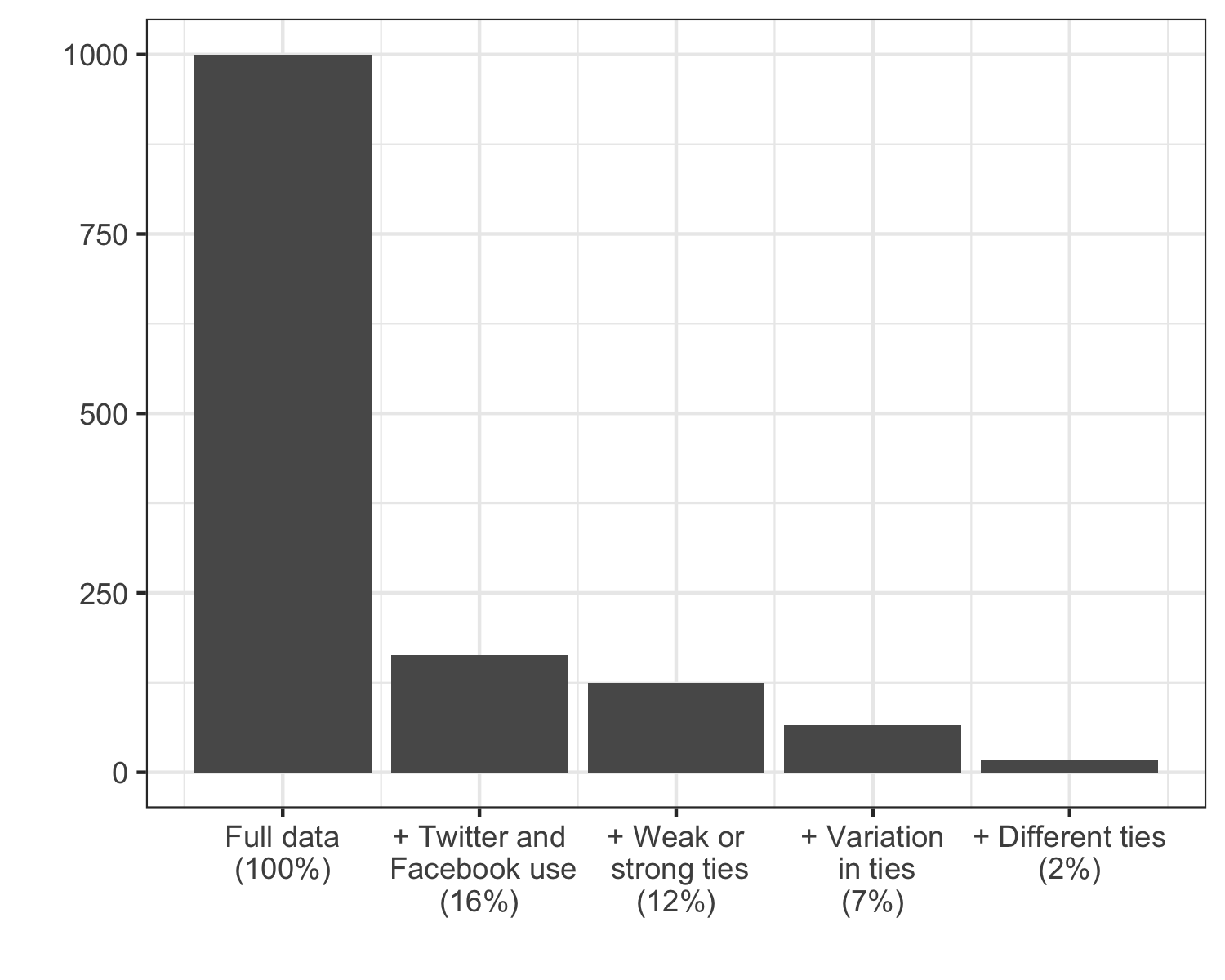
This means that when we enter a regression framework where we begin to control for all of the aforementioned variables, we will be putting a lot of emphasis on very few cases.
Why do we care about this? Because the results are weak (and definitely not strong). Even minor adjustments to the analysis will make these results throw in the towel and beg for mercy. However, this is not the impression you get when you read the paper, and in particular how confident the authors are that the results are representative: “To make the results more representative of the population, all analyses were conducted using a post-stratification weight (although the results are virtually the same when using unweighted data).”
I informed the authors that their findings are not virtually the same when using unweighted data, and that the coefficient for ‘Strong-tie Twitter use’ is actually for ‘Weak-tie Facebook use’ and vice versa. Based on this, the authors issued a corrigendum to the article, stating that: “On Table 1, the study reports regression coefficients for variables in the study. Due to a clerical error, the coefficients for two variables, strong-tie Twitter use and weak-tie Facebook use, are flipped. In Figure 1, however, the same coefficients are correctly displayed. A corrected table appears below. The authors apologize for the confusion this error may have caused.”
Notice how there is nothing about the fact that the results do not hold up when looking at the unweighted data. Interestingly, while not addressing the issue in the text in the corrigendum, the new Table 1 looks nothing like the old Table 1 (i.e. the table presented above). Here is the new table:
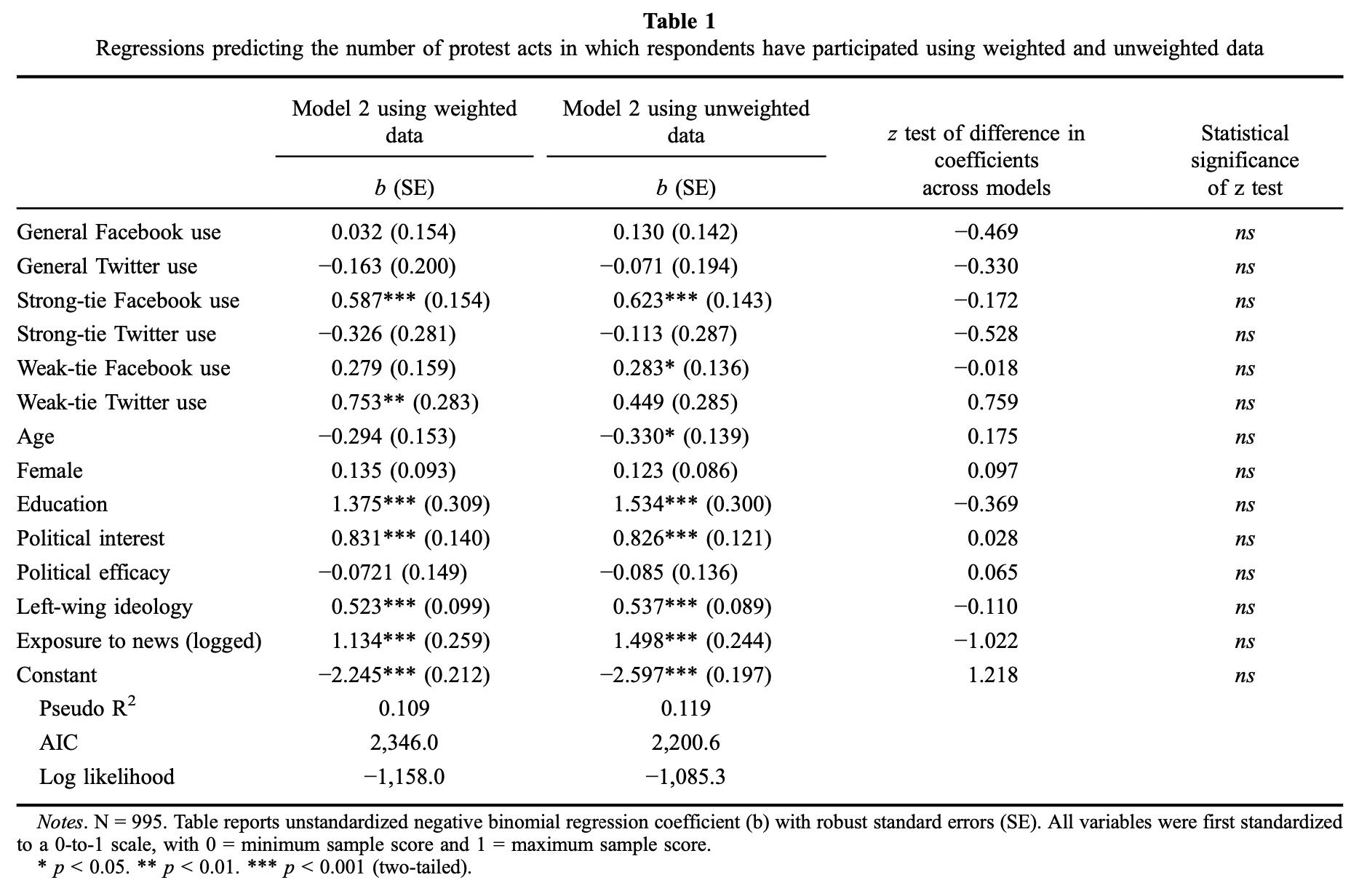
You will see that this table is corrected in a weird manner and looks nothing like the old Table 1. What happened to Model 1? In the new table, we only see two different versions of Model 2. Notice here that, for the unweighted data, neither the strong ties or weak ties on Twitter has a statistically significant effect. Only the two coefficients for ties on Facebook are statistically significant. The same results? No. Virtually the same results? Also no.
Why do the authors say that the results are virtually the same? Because they conduct statistical tests to see whether the coefficients are different across the two models and find no statistically significant differences. This is a very conservative threshold and the coefficients would need to change a lot before they would no longer be “virtually” the same.
However, take a look at the results in the model and see whether they are in line with the key “finding” in the paper. The relevant heuristic here is the following question: Would the authors still have made the same interpretation, i.e. that weak ties matter more than strong ties on Twitter, if only presented with Model 2 using unweighted data? I find that unlikely, especially as the coefficient for weak ties on Facebook is statistically significant in this model.
While there is something predictable about the response from the authors, I do find it interesting that they acknowledge the relevance of reporting the results using unweighted data. Kudos for the transparency, I guess.
What can we learn from this? There might be some methodological recommendations for other researchers who actually care about these issues. First, improve the (effective) sample size. Remember that 1,000 observations might not be 1,000 observations once you are done clicking on fancy buttons in SPSS. This is even more relevant when you might have a lot of measurement error. One study, for example, showed that self-reported Facebook usage is at best correlated .4 with Facebook logs of user activity.
Second, we should care about better sampling (ideally primarily studying social media users). There is no need to have a representative sample if it is limited how much any of these findings actually apply to the representative sample (or the population of interest). I doubt we have learned anything about the relevance of social media from looking at this observational data from a non-representative survey in Chile with limited variation on the key variables of interest.
Third, while we know a lot about social media, there is still a lot to be understood and I would like to see researchers deal with “simpler” hypotheses before turning to complex ideas about how strong and weak ties work across different social media platforms. Sure, it is an interesting idea and I am convinced the authors will spend more time celebrating and promoting their h-index than taking my concerns into account. However, I am – again – not convincend that we have learned a lot about how social media matter upon reading this paper.
There are many challenges with survey data when studying social media, and I am not against using such data at all. Most of my research rely on survey data and I believe we can use such data to say a lot about social behaviour, including on social media. However, there are particular problems that we should be aware of, including what sample we are actually looking at and how that shapes the results we get out of our statistical models.